Bei der Analyse von Geschäftsdaten verlassen wir uns häufig auf Durchschnittswerte und aggregierte KPIs. Sie geben uns einen schnellen Überblick und helfen, Entscheidungen zu treffen. Doch Vorsicht: Manchmal zeigen diese Gesamtübersichten genau das Gegenteil von dem, was in den aufgeschlüsselten Daten steckt - selbst wenn alle Zahlen stimmen! Gerade bei wichtigen Geschäftsentscheidungen ist es daher essentiell, einen genaueren Blick auf die Details zu werfen. In der Statistik nennt man diesen verblüffenden Effekt das Simpson-Paradox.
Besser, aber schlechter? Ein Beispiel aus dem Kundenservice
Wie irreführend Durchschnittswerte sein können, lässt sich am besten an einem konkreten Beispiel zeigen. Schauen wir uns dazu die Performance-Analyse eines Kundenservice-Centers an. Das Unternehmen arbeitet mit zwei Teams: Team A besteht aus erfahrenen Experten, die sich hauptsächlich um komplexe Fälle kümmern. Team B ist das First-Level-Support Team, das überwiegend einfachere Anfragen bearbeitet.
Um das Phänomen zu demonstrieren, habe ich einen fiktiven Datensatz erstellt. Die kompletten Daten sind auf data.world verfügbar.
Die Daten sind auf Fallebene erfasst. Jede Zeile repräsentiert ein bewertetes Ticket mit folgenden Informationen:
- Datum des Tickets
- Zuständiges Team (A oder B)
- Kategorie des Tickets (Complex/Simple)
- Kundenbewertung (1-5 Sterne)
- Flag für hohe Zufriedenheit (bei 4-5 Sternen)
Bei der Performance-Analyse sehen die Gesamtbewertungen erstmal eindeutig aus: Team B erreicht durchschnittlich 3,7 von 5 Sternen, Team A nur 3,4 Sterne.
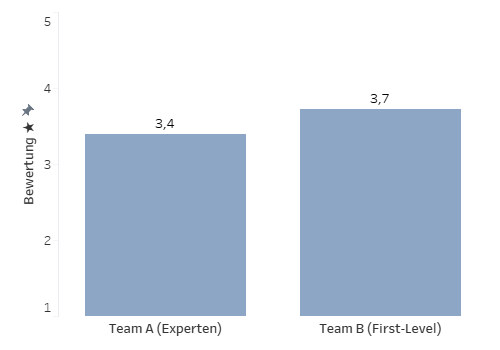
Doch irgendetwas kann hier nicht stimmen: Wieso schneidet ausgerechnet unser Experten-Team schlechter ab als der unerfahrene First-Level-Support?
Die Situation ändert sich jedoch komplett, wenn wir die Bewertungen nach Ticket-Kategorie aufschlüsseln: Plötzlich liegt Team A in beiden Kategorien vorne - sowohl bei komplexen als auch bei einfachen Fällen!
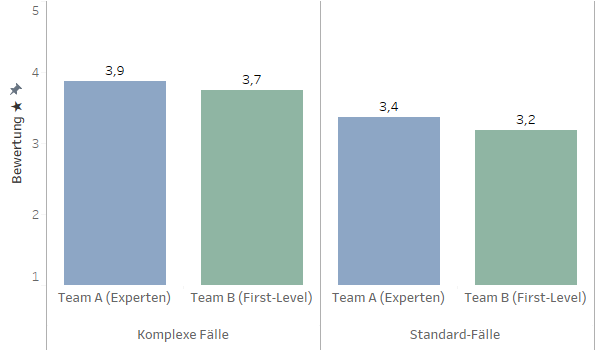
Das entspricht zwar unseren ursprünglichen Erwartungen an das Experten-Team, wirft aber eine neue Frage auf: Was stimmt denn nun?
Der Schlüssel zum Paradox: Die Fallverteilung
Wie lässt sich dieser scheinbare Widerspruch erklären? Der Schlüssel liegt in der Verteilung der Fälle: Team A bearbeitet fast ausschließlich komplexe Fälle (95%), während Team B überwiegend Standard-Fälle betreut (96%).
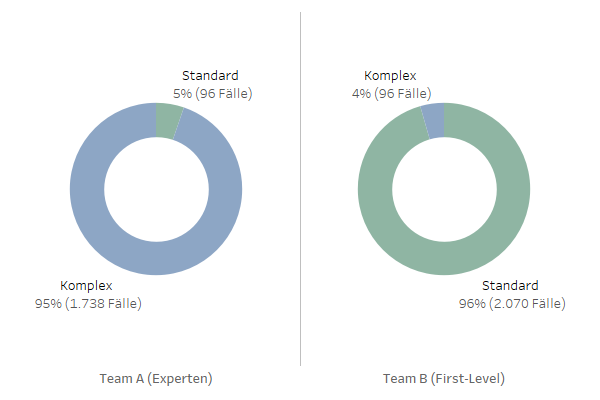
Und genau hier liegt die Erklärung für das Paradox: Da komplexe Fälle generell besser bewertet werden als Standard-Fälle, zieht die ungleiche Verteilung den Gesamtdurchschnitt von Team A nach unten - obwohl sie in beiden Kategorien die besseren Bewertungen erhalten.
Was bedeutet das für die Praxis?
Das Simpson-Paradox zeigt, wie wichtig es ist, Daten im richtigen Kontext zu analysieren. Eine oberflächliche Betrachtung der Gesamtdurchschnitte hätte hier zu gefährlichen Fehlschlüssen führen können - etwa zur Annahme, das Experten-Team leiste schlechtere Arbeit.
In unserem Beispiel war die Lösung nur deshalb so offensichtlich, weil wir die unterschiedlichen Rollen der Teams kannten. Ohne dieses Praxiswissen hätten wir den Widerspruch zu unseren Erwartungen vielleicht gar nicht bemerkt.
Diese Erkenntnis unterstreicht die zentrale Rolle der Kommunikation in der Datenanalyse: Als Analyst muss man die Daten wirklich verstehen - und das geht weit über reine Zahlen hinaus. Woher kommen die Daten? Wie werden sie erfasst? Welche Prozesse stehen dahinter? Diese Fragen lassen sich nur im engen Austausch mit Stakeholdern und den Fachabteilungen beantworten.
Noch kritischer wäre es gewesen, wenn die Unterscheidung zwischen Standard- und komplexen Fällen in den Daten schlicht gefehlt hätte. Gerade hier zeigt sich der Wert von Domain-Expertise: Sie hilft uns nicht nur bei der Analyse bestehender Daten, sondern ermöglicht auch konkrete Empfehlungen für die Zukunft - etwa welche zusätzlichen Informationen erfasst werden sollten, um aussagekräftigere Analysen zu ermöglichen.
Praktische Konsequenzen für die Analyse:
- Vorsicht mit aggregierten KPIs. Eine Aufschlüsselung nach wichtigen Kategorien kann ein völlig anderes Bild zeigen.
- Besonderes Augenmerk auf unterschiedliche Verteilungen in den Daten. Wenn sich Gruppen stark in ihrer Zusammensetzung unterscheiden, sind Gesamtvergleiche oft irreführend.
- Datenvisualisierung auf verschiedenen Ebenen. Der Vergleich von Gesamt- und Detailsicht hilft, solche Paradoxa zu erkennen.
- Einbindung von Domain-Wissen. Oft sind es erst die Kenntnisse aus der Praxis, die uns zur richtigen Interpretation führen.
Fazit: Wenn die Wahrheit nicht im Durchschnitt steckt
Das Simpson-Paradox kommt in der Praxis häufiger vor als man denkt. Der Fall aus dem Kundenservice ist nur ein Beispiel von vielen: Ähnliche Effekte finden sich etwa bei Conversion Rates unterschiedlicher Marketingkanäle oder beim Vergleich von Verkaufszahlen verschiedener Regionen. Ein genauer Blick in die Details lohnt sich also immer - manchmal steckt die Wahrheit eben nicht im Durchschnitt.
