If you're analysing and comparing data across different categories, you might be wondering how to compare different groups of numbers effectively. One handy tool for this is called a z-score.
What Is a Z-Score?
A z-score tells you how far a particular number is from the average (mean) of a group, measured in standard deviations. In simpler terms, it shows how "unusual" or "normal" a number is compared to the rest of the numbers in that group.
Here’s a basic way to think about it:
Average (Mean): This is the typical value in a group. For example, if the average score on a test is 70, most students scored around this number.
Standard Deviation: This indicates how spread out the numbers are. A small standard deviation means the scores are close to the average, while a large one means they are more varied.
The formula for finding a z-score is:
z = (X−average) / standard deviation
Where:
- X is the number you’re looking at,
- Average is the mean of the group,
- Standard deviation measures how spread out the numbers are.
Why Use Z-Scores?
Easy Comparisons: Z-scores help you compare numbers from different groups. For instance, if you want to compare test scores from maths and history, z-scores let you see how each score stands out in its own subject.
Spotting Outliers: If a z-score is very high or very low, it indicates that the number is an outlier, meaning it’s quite different from the rest. This can help identify unusual results, like a student who scored much higher or lower than their classmates.
Different Scales: If you’re comparing things that are measured differently (like scores and sales figures), z-scores put everything on the same scale, making comparisons easier.
Informed Decisions: Businesses can use z-scores to make better choices. For example, if one product has a high z-score for customer satisfaction, it might be worth promoting more.
For example:
If we want to compare the average price of Airbnb apartments in different boroughs in London - we could just use the average price for each borough - as seen below. But this makes it difficult to compare the scores between different room types.
However if we want to see how each borough compares to the average for each room type - we can use z-scores to normalise for each room type and identify outliers.
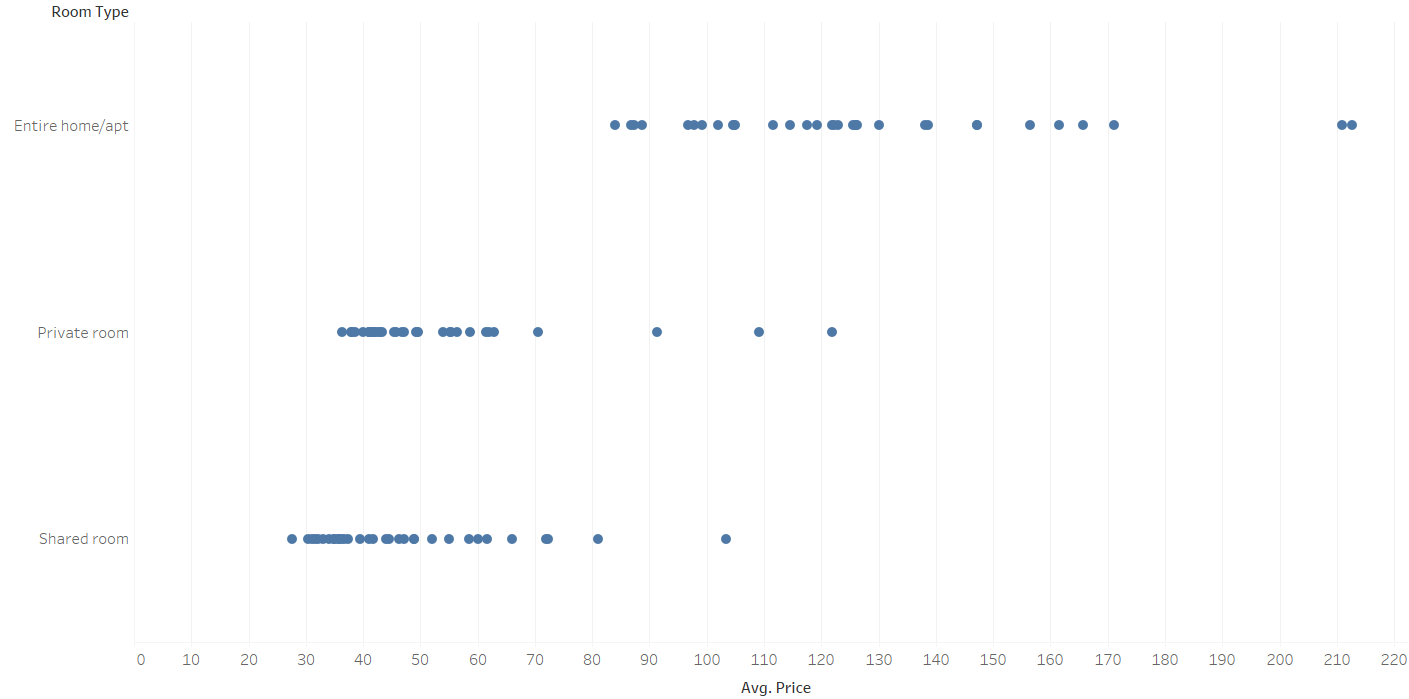
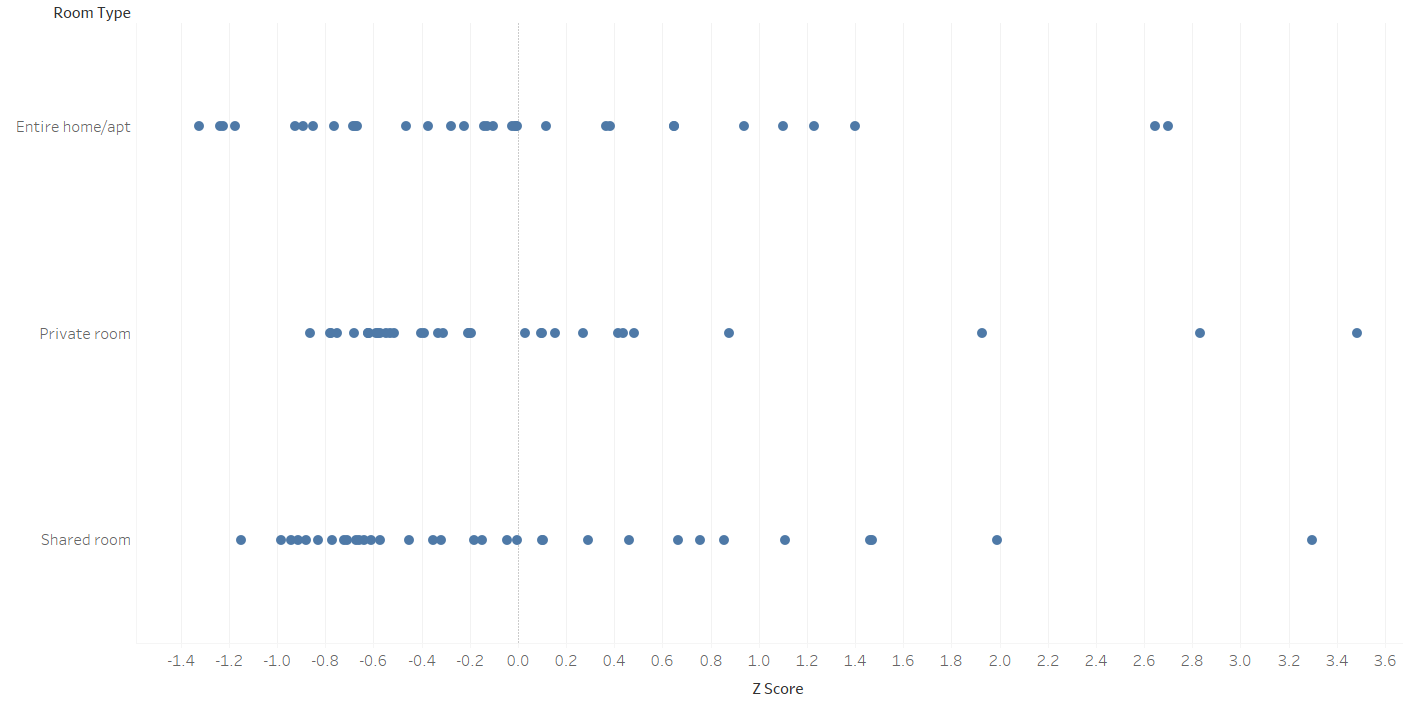
Examples of where you may use Z-Scores:
Test Scores: If in a maths test the average score is 75, with most students scoring between 65 and 85. If you score 90, calculating your z-score shows how well you did compared to everyone else. If the z-score is positive, you did better than average. You could then compare this with other subjects and see who did better relative to their peers in English and Science - even though the average marks for each test may be different - as you are standardising it and comparing it to the distribution rather than just using the pure marks.
Sales Figures: Imagine a shop has an average monthly sale of £20,000 with some variation. If one month they sold £30,000, calculating the z-score shows if this was an exceptional month compared to their usual sales.
Z-scores are a useful way to understand how individual numbers compare to a group. They help you see what’s normal and what’s unusual, making it easier to analyse and make decisions based on data, and compare across different data sets.
