What is a Z-score?
A Z-score (Whether it be Zed or Zee is up to you) is a number that describes a value's relationship to the mean of a group of values. Z-score will be measured in terms of standard deviations from the mean. When the Z-score is 0, it shows that there is no difference between the data point and mean score.
Here is an example to help you understand:
Say we have two gamers, John and Sko.
John gets 125 score in a Pacman game, and Sko gets 160 score in the flappy bird game.
How can we say who performed better in comparison to other gamers playing these games?
We can’t do only by looking at their game scores as the variability in their fellow gamers’ scores might be different
The average scores for each game are as follows with a normal distribution: Pacman has a mean 110 and SD 4 and Flappy bird has a mean 155 and SD 2
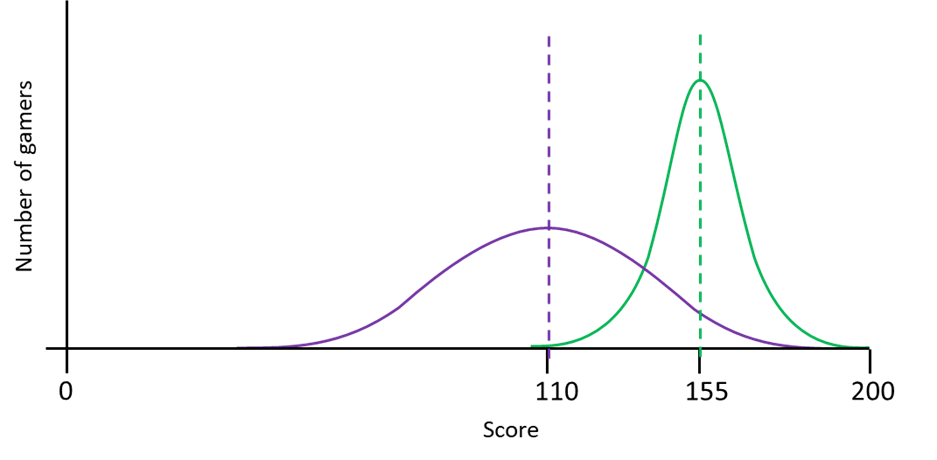
We need to scale our distribution so the mean is 0 and SD is 1
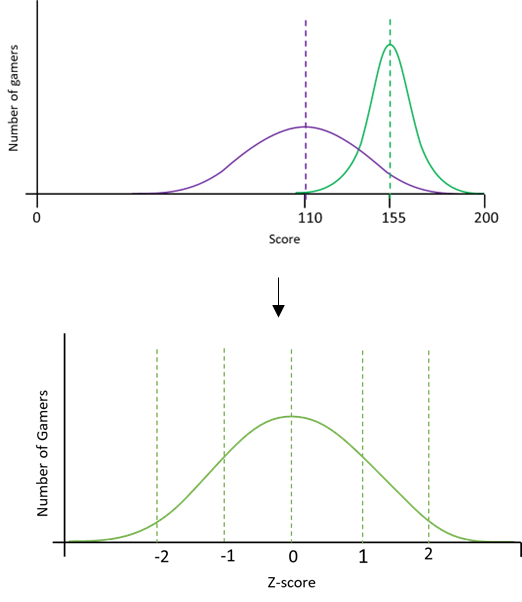
Z-scores are the number of standard deviations away from the mean, the equation used to calculate them is shown below:
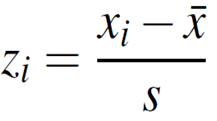
Using the equation we calculate the mean minus the score for each individual and then this is divided by the number of standard deviations.
To remind us again:
The average scores for each game are as follows with a normal distribution: Pacman has a mean 110 and SD 4 and Flappy bird has a mean 155 and SD 2
John got 125 score in a Pacman game, and Sko scored 160 in the flappy bird game
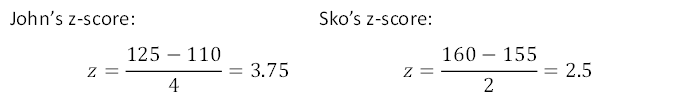
Here we can see our z-scores plotted on a normal distribution:
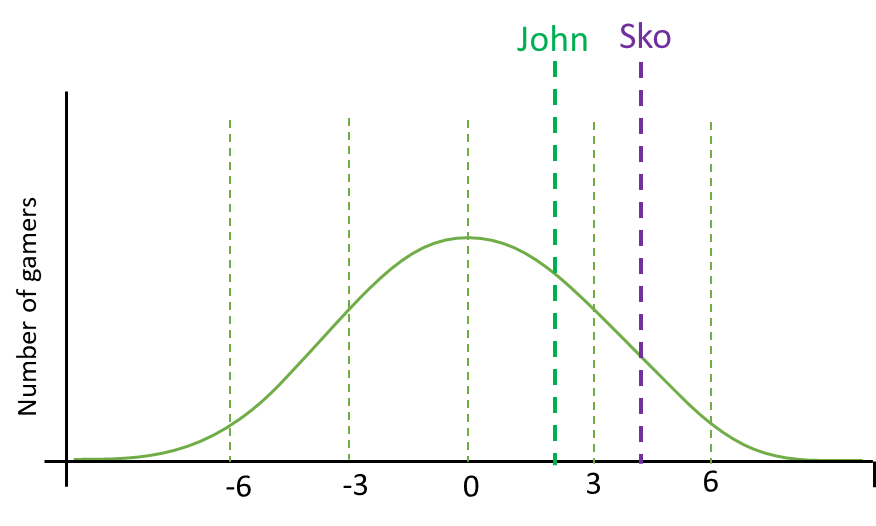
Despite the fact Sko got a higher score than John, we can conclude that John actually performed better at his game when comparing the rest of gamers who also played.
