Regression models are used to describe relationships between variables by fitting a line of best fit through the data points. Regression analysis allows you to explore how a dependent variable changes as the independent variable(s) change.
Regression models can be done as 'simple regression' models where there is a dependent variable and only 1 independent variable or as a 'multiple linear regression' where there are 2 or more independent variables. For this blog we are looking at simple linear regression only
Simple Linear Regression
Simple linear regression is used to estimate the relationship between two quantitative variables, one independent and one dependent variable.
Simple linear regression is a good option when you want to explore how strong the relationship is between two variables. An example of this is seeing the relationship between smoking and life expectancy.
Another reason you may want to use the simple linear regression model is to view the y value of the dependent variable at the point x of our independent variable i.e. the life expectancy when smoking x amount of cigarettes.
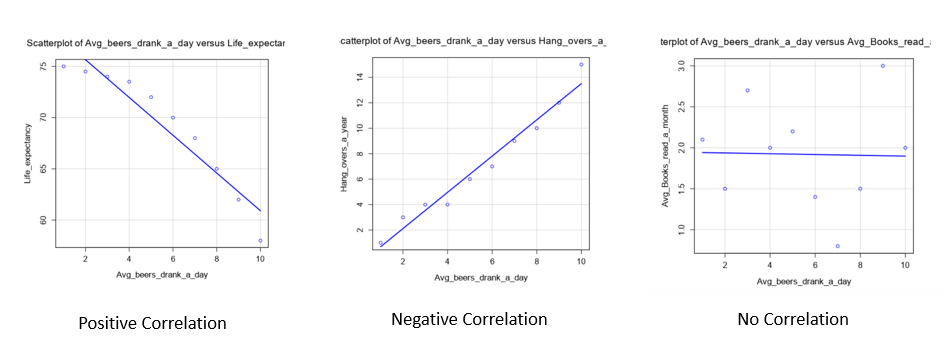
The strength of the relationship between these variables will be done using Person's correlation which has a value between -1 to 1. Where 1 means complete positive correlation and -1 meaning completely negative correlation. It can also have a correlation of 0 which indicates no correlation.
Simple Linear Regression Formula
Simple linear regression formula
The formula for a simple linear regression is:
y =B0 + B1X + e
Where
y - is the predicted value of the dependent variable at a point on the independent variable
B0 - is the intercept when the x-axis = 0. So the point will be (0, B0)
B1 - is the regression coefficient – how much the 'y' will change as a response to a change in x
x - is the independent variable
e - is the error of the estimate, or how far away the point is from the regression line. This will be the difference in the y axis from the point to the regression line. So if x = 3 connects to y=5 on the regression line but the data point at x=3 is actually y = 7 then the 'e' will = 2
The r² value (aka estimate)
The r² value explains how well the regression model explains observed data. For example an r² value of 0.7 would indicate that reveals that 70% of the variability within the model can be explained by the regression line.
There is no universal value used as benchmark for what is a good r² value or what is a bad one. Its all dependant on the use case and research that the analysisis being part of. For human behaviour a lower r² value (0.5, 0.6) may show strong relationship between the two variables as human behaviour is unpredictable and volatile. On the other hand in a pharmaceutical study an r² value of 0.9 although showing a strong relationship, would still be too low and you need absolutes and everything needs to be almost perfect. In some cases where you don't expect perfect r² value, finding one could indicate that somethings wrong with the data and needs investigating. It is purely situational.
For the examples used above alteryx tells us that the r² for the negative correlation table is -0.95339 (95.3%) . This would indicate a very strong relationship between the two as can also be observed by looking at the regression line. The no correlation chart has an r² value of -0.022663 (0.23%) which indicates an extremely weak relationship between the two.
This is just a very basic introduction to simple linear regression and can get a lot more complete when looking at multiple linear regression as well as other regression methods such as the spearman correlation.
